10-14 << Previous Next >> CAD1 繪圖

HW1

HW1 具體項目成果回報區將於 2021.09.23 開啟, 於 2021.11.10 22:00 關閉.

有關機械臂的軌跡線性控制或圓形控制，軌跡調整

閱讀日期10/28 閱讀時間30mins(包含翻譯)、影片長度2分鐘(尚未閱讀完畢)

1.導讀:要介紹使用三個自由度去製作minion機器人，這個影片將會解釋如何使用線性與旋轉去做軌跡控制

2.三大目的:描繪meArm的直線運動學、如何實現機械手臂(在笛卡爾空間)進行直線、旋轉運動，以及完成讓手臂實行點到點控制。

3.解釋各項尺寸

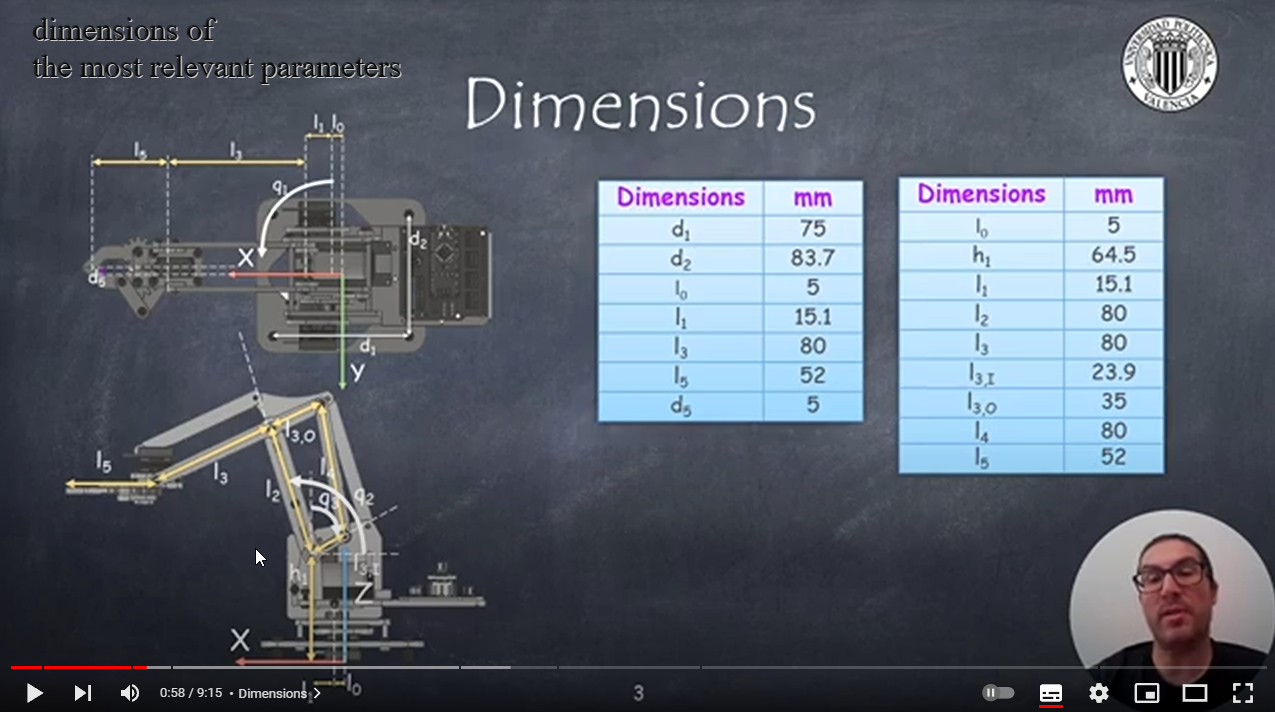
4.直線運動學:第一行解釋如何控制關節讓抓手在x-y象限中移動

首先我們需要先確定r的長度，要注意在機台上的關節軸2,3(也就是上方圖片l2與i3相連的關節)

可以經由簡單的三角函數得到r的長度

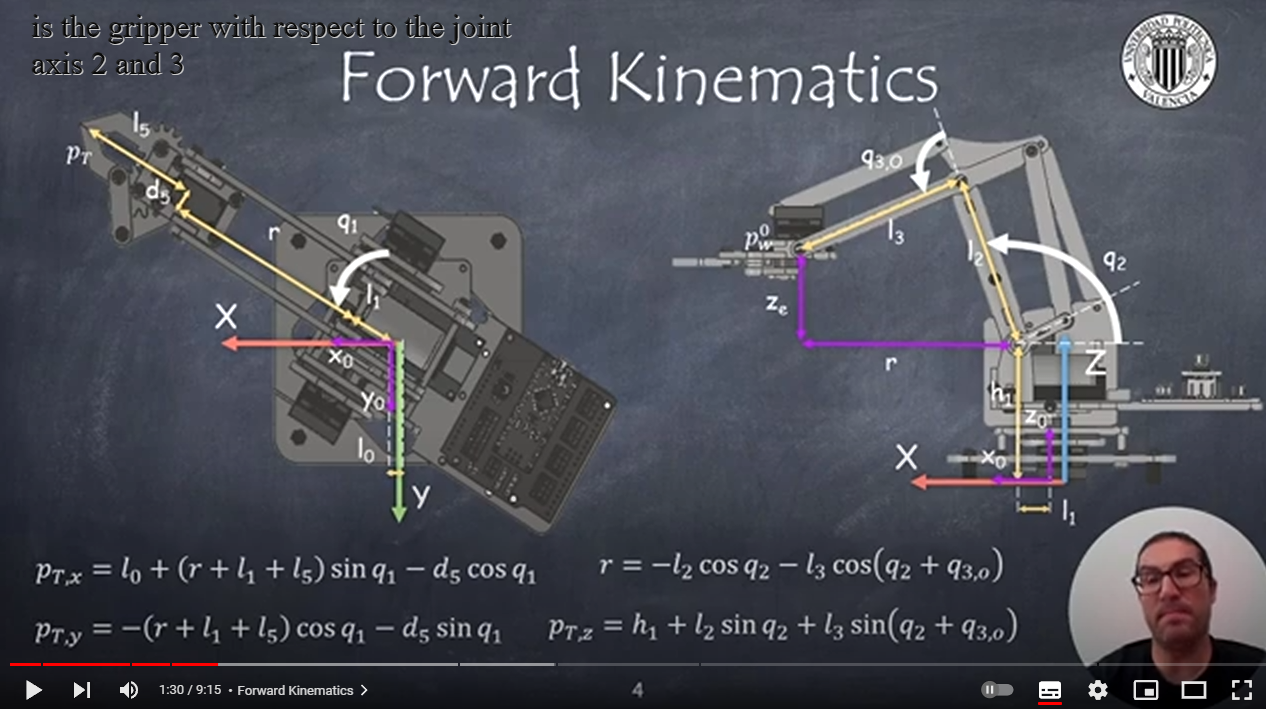接著，我們就可以計算出夾爪在x與y的哪個位置。

值得一提的是，座標計算並不簡潔但卻又很經典的學術例子，因為在計算上，l0與d5並不是0，會影響到座標軸上的計算結果。

閱讀日期11/4 閱讀時間2hr(包含翻譯)、影片長度5分鐘(尚未閱讀完畢)

4-1:直線運動學理論延伸

在z座標上夾爪的高度的調整是由q2角度與q3o角度而定，並且與簡單的三角函數相關。

q3o角度的計算可以知道是從四連桿結構去計算，如下圖

4-2:直線運動軌跡計算

倘若你希望讓夾爪以線性方式進行移動，如同使從p0抵達pt，則是以一種三次式的軌跡進行移動

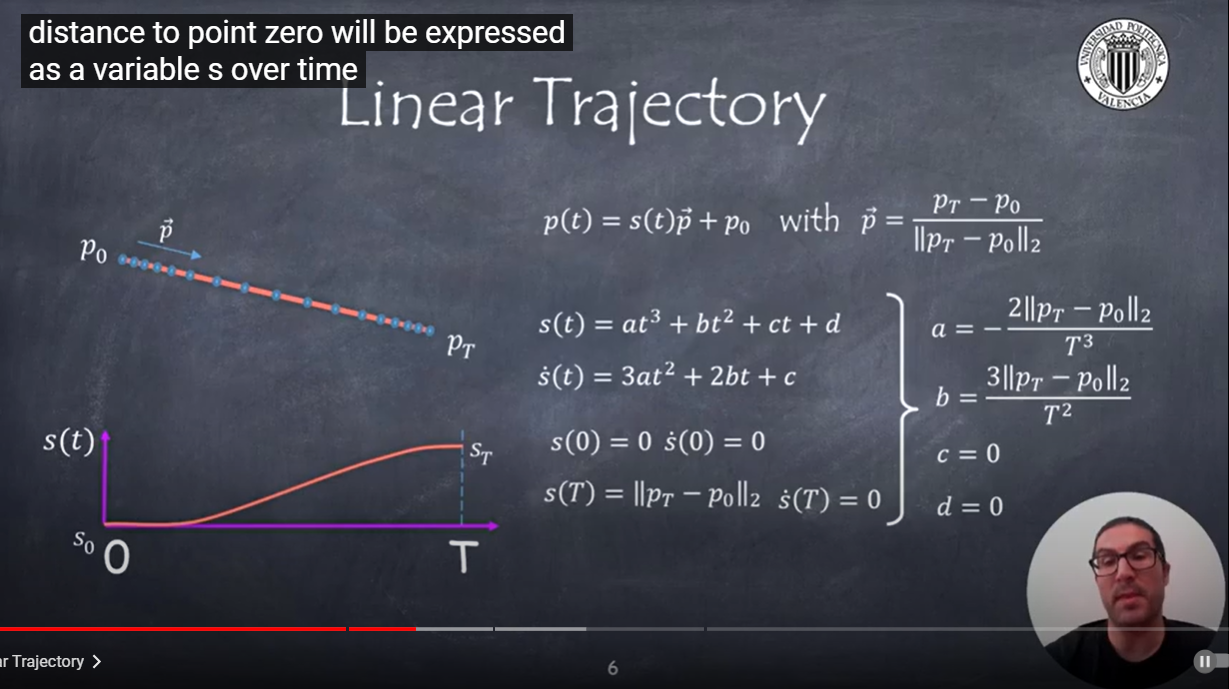
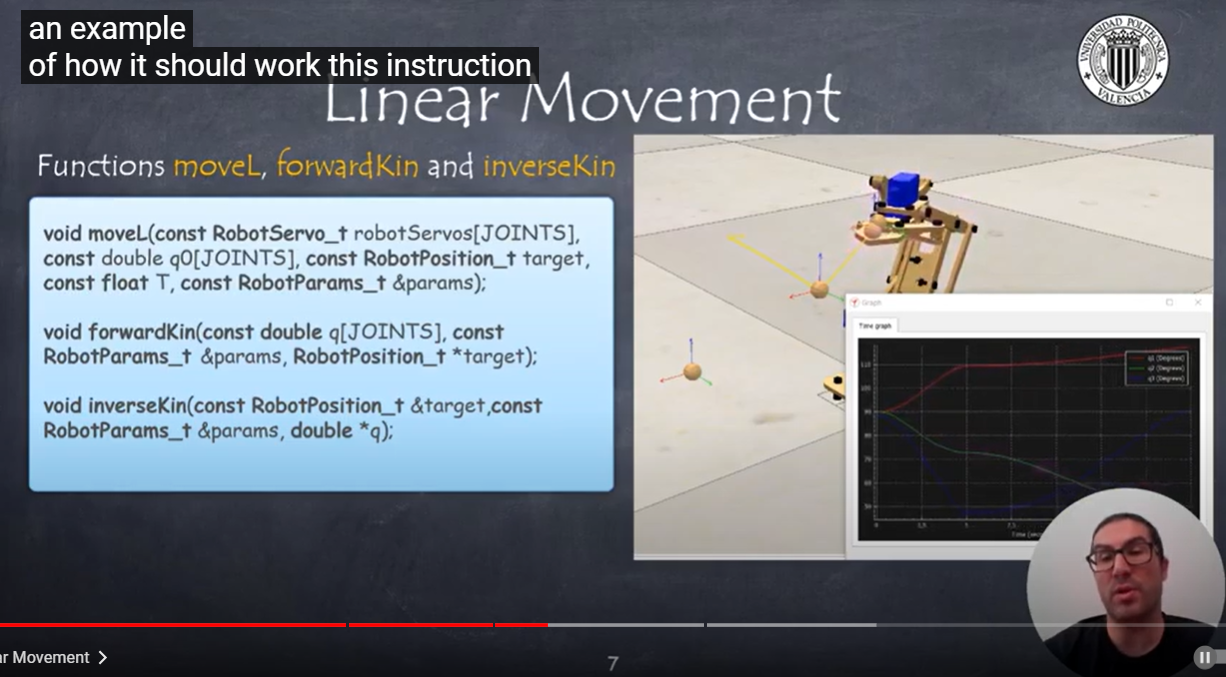
4-3:直線運動實踐

當開始實行直線移動的時候，我們能夠看到，在笛卡爾座標-三角座標軸系統中，夾爪在這裏面的移動模式。

從這可以發現，在這一段移動的動畫中使用三個指令，分別是movel forwardKin inverseKin，都能夠提供夾爪在三角座標軸上的移動論證
並且我們也必須要提供這些數據與時間t的關係，提供初始時間與最終時間

簡而言之，就是提供初位置、末位置、初時間與末時間，最後我們就能在三角座標軸上得到線性運動。

5.旋轉運動學:

1. CAD 套件分配表:

sw: Solidworks, inv: Inventor, nx: NX12, ons: Onshape, slvs: Solvespace

2. 在兩套 CAD 完成零件繪圖並轉入 CoppeliaSim 後, 為了建立 Dynamic Model 必須利用 shape edit modes 轉為 clean model, 並與實際轉入的 STL 格式零件外形結合應用後建立模擬場景 (scenes).

3. meARM Robot 動態模擬場景的建構, 可參考 0, 1, 2, 3, 4, 5, 6, 7, 也可參考 Uarm Robot model 與相關影片.

4. CoppeliaSim design dynamic simulations 說明頁面.

5. 網際 Lua 程式執行.

10-14 << Previous Next >> CAD1 繪圖